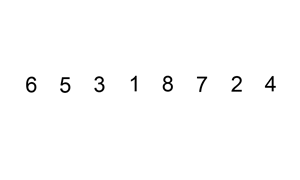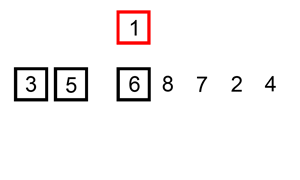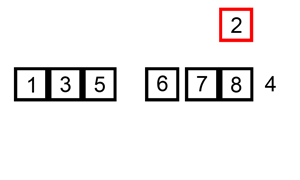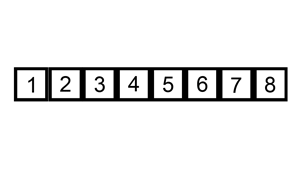C Insertion Sort

Summary: This tutorial introduces you to the insertion sort algorithm and how to implement the insertion sort in C.

Introduction to insertion sort algorithm #

In the insertion sort algorithm, we sort an unsorted array by inserting its elements into the proper positions in a sorted array. The insertion sort algorithm is efficient if the array is substantially sorted. However, it is more efficient to use the quicksort or heapsort algorithm to sort a big list of unsorted elements.

When we sort something manually, we often use the insertion sort technique, e.g., when we sort a deck of playing cards. We can describe the insertion sort algorithm as similar to sorting a deck of playing cards:

1. First, we start with an empty set of cards (the sorted array on our hand) and the unsorted array on the table.
2. Then we pick one card at a time from the table, i.e., the unsorted array,  and insert it into the proper position in our hand  i.e., the sorted array
3. To insert a card in the correct position, we compare it with the existing cards in our hand from right to left.

Notice that the cards that we hold are always sorted.

The complexity of the insertion sort algorithm is О(n²), where n is the number of elements to be sorted.

C insertion sort algorithm implementation #

The following is the program that demonstrates the insertion sort in C.

#include <stdio.h>
#include <stdlib.h>

#define SIZE 10
void swap(int *a, int *b);
void insertion_sort(int *a,const int size);

int main()
{
    int a[SIZE] = {3, 4 , 6, 1, 5, 8, 7, 9, 0, 2};

    insertion_sort(a, SIZE);

    int i;
    for(i = 0; i < SIZE; i++)
    {
        printf("%d ",a[i]);
    }
    return 0;
}

void swap(int *a, int *b)
{
    int temp = *a;
    *a = *b;
    *b = temp;
}
void insertion_sort(int *a,const int size)
{

    int i,j, k;
    for (i = 1; i < size; ++i)
    {
        k = a[i];
        j = i - 1;
        while ((j >= 0) && (k < a[j]))
        {
            a[j + 1] = a[j];
            --j;
        }
        a[j + 1] = k;
    }
}Code language: C++ (cpp)

In this tutorial, we have explained the insertion sort algorithm and shown you how to implement it in C.