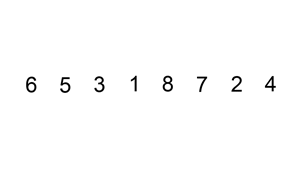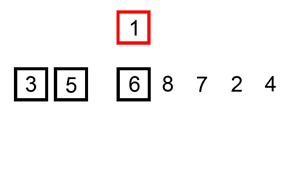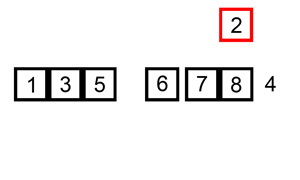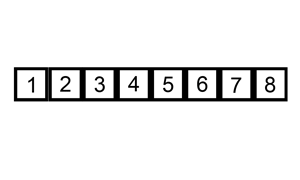C Insertion Sort

Summary: this tutorial introduces you to insertion sort algorithm and how to implement the insertion sort in C.

Introduction to insertion sort algorithm

In the insertion sort algorithm, we sort a unsorted array by inserting its elements to the proper positions in a sorted array. The insertion sort algorithm is efficient in case the array is substantially sorted. It is more efficient to use the quicksort or heapsort algorithm to sort a big list of unsorted elements.

When we sort something manually, we often use the insertion sort technique e.g., when we sort a deck of playing cards. We can describe the insertion sort algorithm similar to sort a deck of playing cards:

1. First, we start with an empty set of cards (on our hand i.e., the sorted array) and the cards on the table i.e., the unsorted array.
2. Then we pick one card at a time from the table i.e., unsorted array,  and insert it into the proper position in our hand  i.e., the sorted array
3. In order to insert a card in the correct position, we compare it with the existing cards in our hand from right to left.

Notice that the cards that we hold are always sorted.

The complexity of the insertion sort algorithm is О(n²) where n is the number of elements that need to be sorted.

C insertion sort algorithm implementation

The following is the program that demonstrates the insertion sort in C.

#include <stdio.h>
#include <stdlib.h>

#define SIZE 10
void swap(int *a, int *b);
void insertion_sort(int *a,const int size);

int main()
{
    int a[SIZE] = {3, 4 , 6, 1, 5, 8, 7, 9, 0, 2};

    insertion_sort(a, SIZE);

    int i;
    for(i = 0; i < SIZE; i++)
    {
        printf("%d ",a[i]);
    }
    return 0;
}

void swap(int *a, int *b)
{
    int temp = *a;
    *a = *b;
    *b = temp;
}
void insertion_sort(int *a,const int size)
{

    int i,j, k;
    for (i = 1; i < size; ++i)
    {
        k = a[i];
        j = i - 1;
        while ((j >= 0) && (k < a[j]))
        {
            a[j + 1] = a[j];
            --j;
        }
        a[j + 1] = k;
    }
}
Code language: C++ (cpp)

In this tutorial, we have explained the insertion sort algorithm and shown you how to implement the insertion sort in C.